0から始める構造力学　[静定ラーメンの応力図]

本日は静定ラーメンの応力図を解説していきます。
応力図が描けるようになれば、応力がどのように材を伝わっていくのかをイメージできるようになります。
しっかり基本的な考え方を学習していきましょう。

Contents

下図の静定ラーメンの応力図を求めよ。

①支点に反力を仮定する
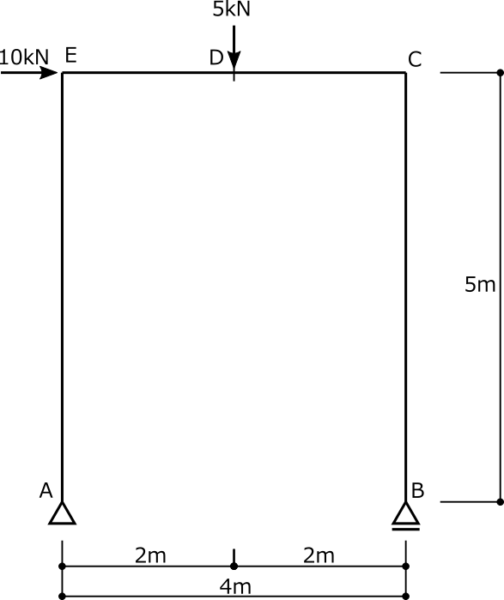
②力のつり合いを考えて反力を求める
③応力を求めたい点で部材を切断し、片側部分を取り出し、切断面に応力を仮定する。
④力のつり合いを考えて、曲げモーメント、せん断力、軸方向力を求める。

①支点に反力を仮定する

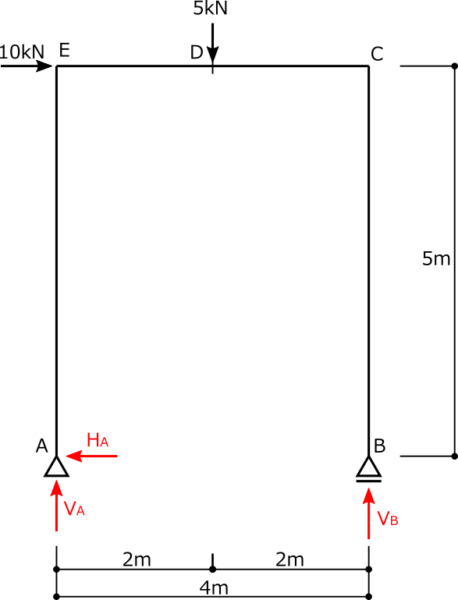
②力のつり合いを考えて反力を求める

ΣX=0より
\(10-H_A=0\)
\(H_A=10\) [kN]

ΣY=0より
\(V_A+V_B-5=0\)・・・①

\(ΣM_A=0\)より
\(10×5+5×2-V_B×4=0\)
\(V_B=15\) [kN]

①に\(V_B=15\)を代入
\(V_A+15-5=10\)
\(V_A=-10\) [kN]

\(V_A\)が(－)なので仮定と逆向きの下向きとなる。

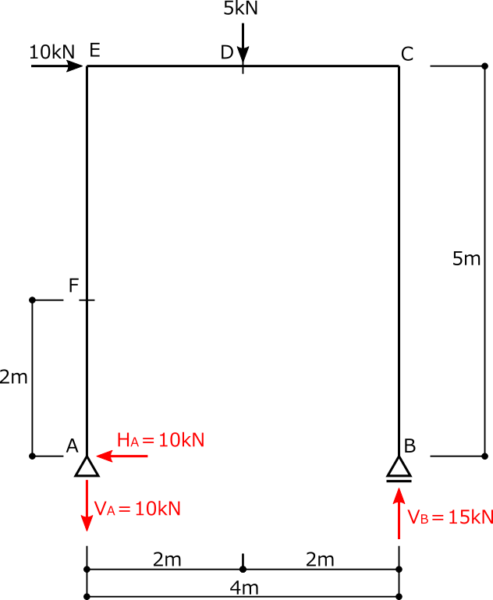
③応力を求めたい点で部材を切断し、片側部分を取り出し、切断面に応力を仮定する。

ももうさ

今回は応力の流れを理解するために、AE材をA点から2ｍの位置で切断してみます。

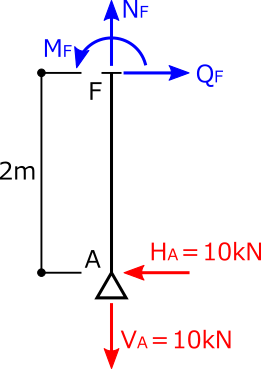
④力のつり合いを考えて、曲げモーメント、せん断力、軸方向力を求める。

ΣX=0より
\(-10+Q_F=0\)
\(Q_F=10\) [kN]

ΣY=0より
\(-10+N_F=0\)
\(N_F=+10\) [kN]　(引張力)

Σ\(M_F\)=0より
\(10×2-M_F=0\)
\(M_F=20\) [kN・m]

ももうさ

支点の片側だけ取り出して任意の位置の応力を求めてみると次の特徴がわかります。

①軸方向力とせん断力は材間で反力が一つだけの場合、材間のどの位置でも一定の値となる。
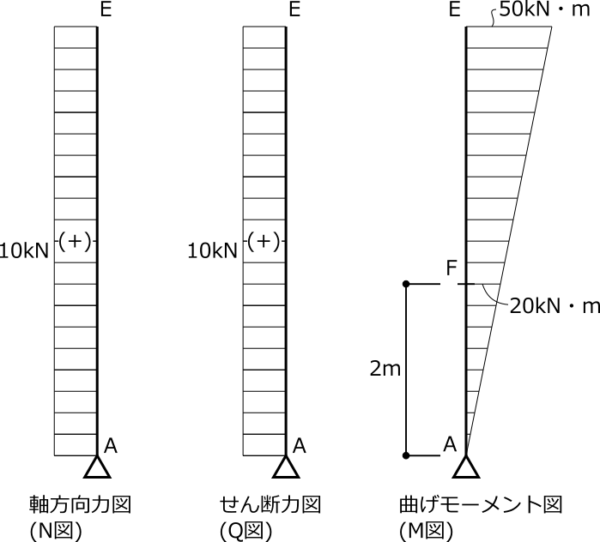
②曲げモーメントは、せん断力に垂直距離をかけた値となる。ピン支点では0から始まり、直線的に増加し、せん断力の大きさが傾きとなる。

ももうさ

次はD点で切断し、左側を取り出して応力を求めてみましょう。

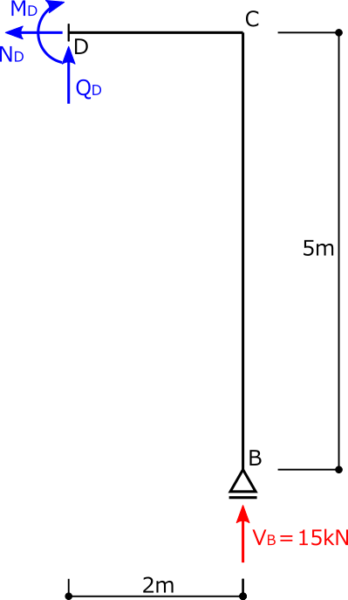
ΣX=0より
\(N_D+10-10=0\)
\(N_D=0\) [kN]

ΣY=0より
\(-10-Q_D=0\)
\(Q_D=-10\) [kN]　(-なので、反時計まわり(↓↑)の組み合わせ)

Σ\(M_D\)=0より
\(10×5-10×2-M_D=0\)
\(M_D=30\) [kN・m]

ももうさ

この計算結果から、E点からD点に向かうほど、下向きの反力\(V_A\)の垂直距離が長くなるので、反時計回りのモーメントが強くなることがわかります。

D点から右側の応力も考えてみよう。

とまとねこ

ももうさ

まずBC間に注目すると軸力(圧縮力)しかないことがわかります。今までの応力の特徴から、BC間にはモーメントが発生しないことがわかります。
次にD点の応力ですが、C点からD点に向かうほど、上向きの反力\(V_B\)の垂直距離が長くなるので、反計回りのモーメントが強くなることがわかります。

ΣX=0より
\(N_D=0\) [kN]

ΣY=0より
\(15+Q_D=0\)
\(Q_D=-15\) [kN]　(-なので、反時計まわり(↓↑)の組み合わせ)

Σ\(M_D\)=0より
\(M_D-15×2=0\)
\(M_D=30\) [kN・m]

まとめ
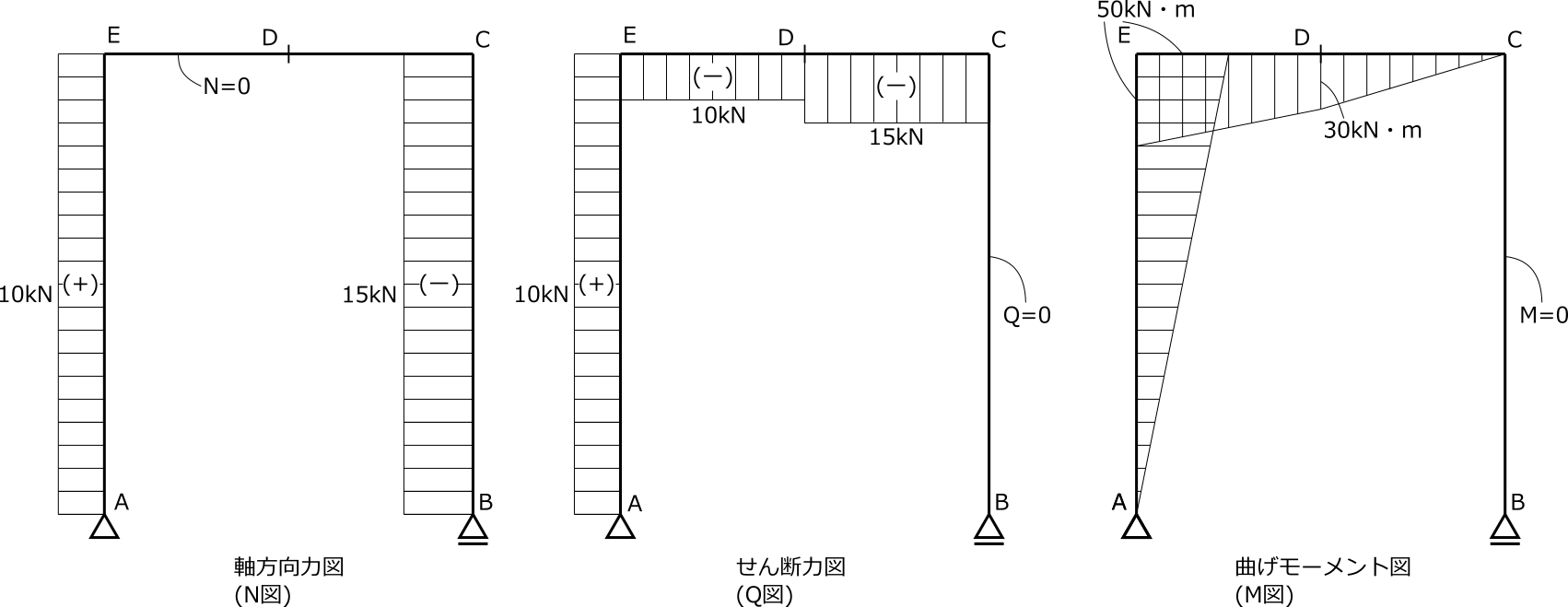
剛接合は曲げモーメントを伝達する。
曲げモーメントの傾きは、せん断力の大きさで決まる。

構造計算の基本から学べる講座を2/22(土)に開催いたします。

アウトプットを重視した内容になっているので、わからないところを直接、講師の先生に聞くことができます。
講座までにわからないところをまとめて、理解不足の項目を効率よく学習しましょう。

構造力学は手順をしっかり理解すれば、解ける問題が格段に増えます。
この講座で構造計算を得点源にしていきましょう。