今回は3ヒンジラーメンについて手順を解説していきます。
覚えるべき手順はとても少ないので、しっかり覚えて確実に得点できるように練習しましょう。

Contents
3ヒンジラーメン
図のような荷重が作用する3ヒンジラーメンにおいて、A点における水平反力\(H_A\)の大きさを求めよ。
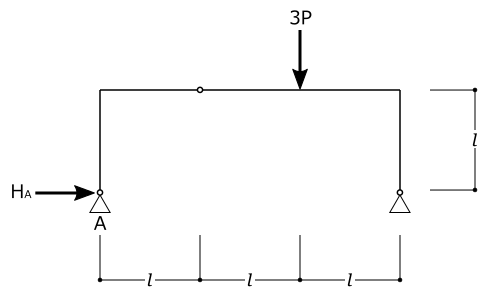
①支点に反力を仮定する
②求めたい支点と反対の支点でモーメントのつり合い式を立てる(逆支点)
③ピン節点の片側部分のモーメントのつり合い式を立てる(ピン片)
②求めたい支点と反対の支点でモーメントのつり合い式を立てる(逆支点)
③ピン節点の片側部分のモーメントのつり合い式を立てる(ピン片)
ももうさ
覚えるべきポイントはたった二つ
逆支点とピン片!
逆支点とピン片!
①支点に反力を仮定する
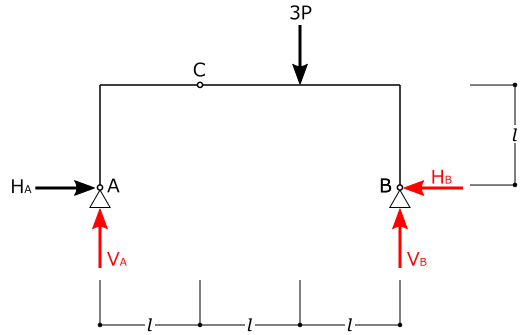
②求めたい支点と反対の支点でモーメントのつり合い式を立てる(逆支点)
ももうさ
求めたい支点と反対の支点でモーメントのつり合い式を立てることで、求めたい支点まわりの未知数を減らすことができます。
\(\Sigma M_B=0\)より
\(V_A \times 3l − 3P \times l = 0\)
\(V_A = P\)
③ピン節点の片側部分のモーメントのつり合い式を立てる(ピン片)
ももうさ
ピン節点は必ずモーメントが0になるという性質を利用して、\(H_A\)を求めます。
一度、取り出した図を描いてみましょう。
一度、取り出した図を描いてみましょう。
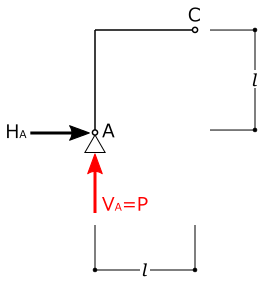
\(\Sigma M_{C左}=0\)より
\(V_A \times l − H_A \times l = 0\)
\(H_A = V_A\)
[\(V_A = P\)]を代入して
\(H_A = P\)
ポイントさえ覚えれば、他の3ヒンジラーメンの問題も解けるよ。
挑戦してみよう。
挑戦してみよう。
とまとねこ
アウトプット型講座 [構造]
構造計算の基本から学べる講座を2/22(土)に開催いたします。
アウトプットを重視した内容になっているので、わからないところを直接、講師の先生に聞くことができます。
講座までにわからないところをまとめて、理解不足の項目を効率よく学習しましょう。
構造力学は手順をしっかり理解すれば、解ける問題が格段に増えます。
この講座で構造計算を得点源にしていきましょう。


