今回は音響について基本的な性質を中心に解説していきます。
音は目に見えない現象なのでイメージするのが難しい分野ですが、
基本的な性質を理解することで、イメージもしやすくなります。
普段生活している中での身近な音をイメージしながら覚えましょう。

音の基本的性質
空気分子を次々に揺らして、空気中を伝わる波を音波といいます。この波が人間の耳の鼓膜を揺らすと人間はそれを音として感知します。
揺れながら伝わる過程で、空気分子が粗と密になる部分ができます。それを粗密派と呼びます。
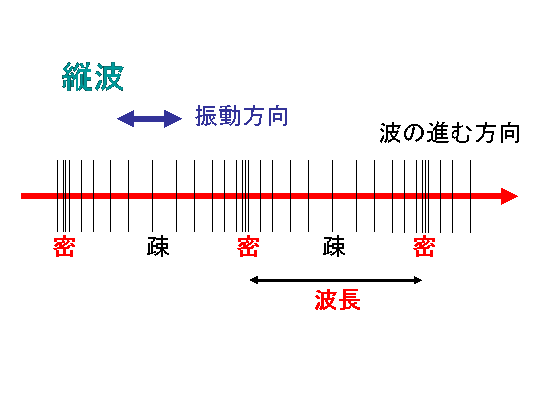
周波数:粗密の1秒間の繰り返しの回数[Hz]
この繰り返しの回数が多いものが高周波音
繰り返しの回数が少ないものが低周波音
となります。
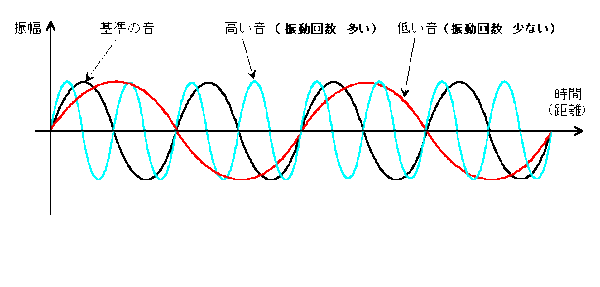
周波数の高い音:救急車のサイレン音
周波数の低い音:花火の音
とイメージしましょう。
波長:粗密の1サイクルにおける長さ
つまり、
高周波音は波長が短くなり、
低周波音は波長が長くなります。
空気中での音速は 331.5m/s で、1℃ 上昇するごとに 0.6m/s ずつ増加します。
C=331.5 + 0.6t
C:音速[m/s]
t:気温[℃]
回折とは障害物の後ろに回り込んで音が聞こえる現象のことをいいます。
高周波音は直進性が高いという性質があります。
そのため障害物にぶつかると音は遮蔽されやすいです。
低周波音は回折性が高く、障害物があっても回り込んで音が聞こえるという現象が起きます。
花火の音(低周波音)は周りに高層ビルなど障害物があっても聞こえてくる。
とイメージして覚えましょう。
音の3要素
音の大きさは、物理的な強弱でいう音圧で表すことができます。
しかし人間の耳で聞く音の大きさは音圧だけではなく、周波数が大きく影響しています。
人間の可聴範囲は、概ね20~20000Hzの間とされています。
最もよく聞こえる周波数は3000~4000Hz付近になります。
音の高さは周波数で表すことができます。
人間は周波数(振動数)の大きい音を高い音と感じ、周波数の小さい音を低い音と感じます。
ピアノの鍵盤の真ん中のドの音の周波数が 261.6Hz くらいで、その5つ右の鍵盤のラの音の周波数が 440Hz です。
音色は波形の違いによります。
同じ高さの音、つまり同じ振動数の音であっても音を出すものによって違う音に聞こえます。この音波の波形のことを音色(ねいろ)といいます。
同じ高さの音でも、ピアノとバイオリンでは波形が異なるので違う音色に聞こえます。
音の物理的単位
$$I = \frac{W}{4 \pi r^2} [W/㎡]$$
I:音の強さ[w/㎡]
W:音響出力
r:距離
\(4 \pi r^2\)とは、球の表面積です。
つまり音は球状に広がっていきながら、減衰していくことを表しています。
音の強さは距離の2乗に反比例する、ということです。
音圧
音の強さと音圧の関係は下式で表すことができます。
$$I = \frac{P^2}{\rho c} [W/㎡]$$
P:音圧[pa]
\(\rho\):空気密度[kg/㎥]
c:音速[m/s]
音の強さは音圧の2乗と比例関係にある、ということです。
音のレベル表示
音の物理的単位は距離の2乗に反比例して小さくなっていきます。
それを人間の可聴範囲で表すと\(10^{-12}\)~1W/㎡となり大きく桁数が異なります。
そこで音の分野ではそれらの数値を見やすくするため物理量をレベルで評価します。
$$L_I = 10log_{10} \frac{I}{I_o} [dB]$$
\(L_I\):音の強さレベル
\(I\):音の強さ[w/㎡]
\(I_o\):\(10^{-12}\) [W/㎡]
常用対数を10倍した値を用いる
\(I_o\)を基準とした値(可聴範囲の下限値)
①\(a^x=b\)のとき、x のことを指数と言います。
指数は、主に「a を x 乗したらいくつになるか?」を考えるときに使います。
これに対し
②\(x=log_a b\)のとき、x のことを対数と言います。
対数は、主に「a を何乗したら b になるか?」を考えるときに使います。
意味は同じですが視点が異なります。
つまり「何乗したら」の部分をピックアップしているのが対数になります。
10を底とする対数は常用対数と呼ばれます。
$$常用対数:log_{10}A $$
10を何乗したらAになるのか、ということです。
$$log_{10}1 = 0$$
$$log_{10}2 = 0.301$$
$$log_{10}10 = 1$$
となります。
これだけ覚えておけば、
この結果を10倍にしたものが、音の強さレベル[dB]となります。
基準値\(I_o\)(\(10^{-12}\))と音の強さIが同じになったとき
$$10log_{10}\frac{1}{1} = 0 [dB]$$
音の強さレベルは、0dBになる。
基準値より2倍音が強くなれば、3dB
$$10log_{10}\frac{2}{1} = 3 [dB]$$
基準値より4倍音が強くなれば、6dB
基準値より10倍音が強くなれば、10dB
$$10log_{10}\frac{10}{1} = 10 [dB]$$
基準値より100倍音が強くなれば、20dB
基準値より1000倍音が強くなれば、30dB
となります。
人間の感覚量は、物理的刺激量の対数にほぼ比例します。
dBの数値が上がれば、数値に比例して音が大きく聞こえるということです。
音の強さが2倍になると音の強さレベルは+3dB
距離が2倍離れると、
音の強さは距離の2乗に反比例するので
音の強さIは1/4倍になる
つまり、
音の強さレベルは、1/2倍×1/2倍
-3dB-3dB=-6dB
となる。
ラウドネスレベル(音の大きさレベル)
ウェーバー・フェフィナーの法則に基づいた音の強さレベルは、音の物理的単位になります。
実際に人間の耳に聞こえる音の大きさは、周波数によって大きく影響を受けます。
ある音の大きさを、感覚的に同じ大きさと感じる1000Hzの純音の音圧レベル値によって表したものをラウドネスレベル[phon]といいます。
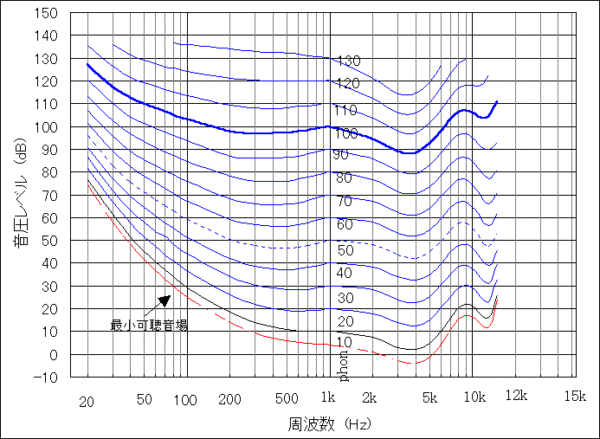
ラウドネスレベルは等高線で表されています。
つまり地図の標高と同じ考え方で読み取っていきます。
X軸方向に周波数を定め、Y方向に音圧レベルを定めます。
二つの値が交差する点が地図で言うところの標高になります。
例えば、
60dBで100Hzの場合、
50phonの等高線上に乗っかているので50phonの大きさで聞こえる
60dBで1000Hzの場合、
60phonの等高線上に乗っかているので60phonの大きさで聞こえる
60dBで4000Hzの場合、
70phonの等高線上に乗っかているので70phonの大きさで聞こえる
ということです。
このことから人間の耳には周波数が高くなれば、音は大きく聞こえるようになることがわかります。
それが最大になる周波数は3000Hz~4000Hzであるということです。
音の強さレベル[dB]と音の大きさレベル[phon]は物理的量と感覚的量の違いであり、混同しないように注意して覚えましょう。
まとめ
音は目に見えない現象なので、まずは高周波音と低周波音の音の特性についてしっかりイメージをつけましょう。
対数の計算は難しいので、基本的な知識だけしっかり身につけましょう。
