環境　圧力差、風力、温度差換気

今回は換気の式について詳しく解説していきます。
取り上げる式はみんな難しいものばかりです。
ですが、式の意味を理解してしまえば実はそんな難しいことは問われません。
しっかりそれぞれの式の言いたいことを考えて覚えていきましょう。

圧力差換気

開口部の前と後で圧力差があると、空気は流れます。
その時、通過する空気量は次式で表されます。

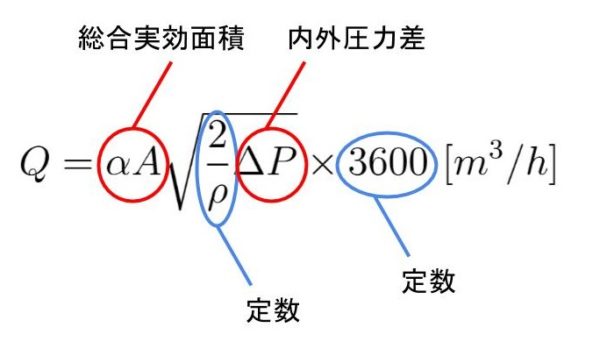
Q：開口を通過する空気量（換気量）[㎥/h]
\(\Delta P\):開口部前後の圧力差　[Pa]
\(\rho\)：空気密度（≒1.2）[kg/㎥]
\(\alpha\)：流量係数
A：開口面積
\(\alpha A\)：総合実行面積[㎡]

まず環境の学科試験において、換気量の式は条件の違う室の換気量の大小関係が問われます。
つまり、全部を計算する必要はなく、定数の部分を無視して考えることが出来ます。
数値が変化するところは赤で囲った\(\alpha A\)と\(\Delta P\)のみです。
その二つの意味をしっかり理解しましょう。

総合実行面積とは開口部の形によって、空気の流れる量が変化するということを表しています。

ベルマウス形状：流量係数\(\alpha\)　1.0
開口断面が滑らかに縮小している形

通常の窓：流量係数\(\alpha\)　0.6～0.7
端部が直角な窓

実際の試験ではこの流量係数\(\alpha\)が変化する（窓の形状が問われる室によって違う）ことはないと考えていいでしょう。
流量係数\(\alpha\)が変化しない、また定数を考えなくて良いとすると、圧力差による換気量の大小関係は、

\(\LARGE 換気量=窓面積\sqrt{圧力差}\)

と簡単に表すことができます。

風力換気

圧力差で空気が流れるのと同じく、風圧の差でも空気は流れます。
その時、風上側と風下側の圧力の大きさを風圧係数を使って表すと次式になります。

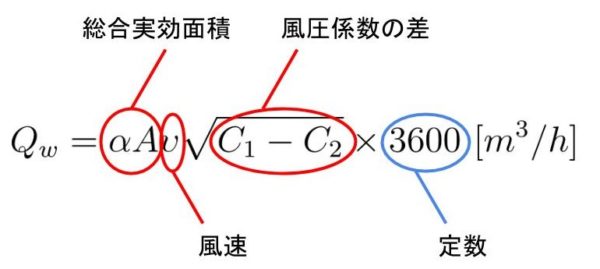
\(\upsilon\)：風速 [m/s]
\(C_1\)：風上側風圧係数
\(C_2\)：風下側風圧係数

前の圧力差換気の式と比べると、風速\(\upsilon\)が増えたのと、圧力差\(\Delta P\)が風圧係数の差\((C_1-C_2)\)に変わっただけです。
風力による換気量の大小関係は、

\(\LARGE 換気量=窓面積×風速\sqrt{風圧係数の差}\)

と表すことができます。

温度差換気（重力換気）

空気は温度が高くなると軽くなり、低くなると重くなります。
また開口部の位置に高低差がある場合、圧力差により空気が流れます。
その二つを考慮した式は、次式で表されます。

h：開口部の高低差 [m]
\((t_i-t_o)\)：室内外の温度差 [℃]
\(T_i\)：室内の絶対温度 [K]

室内の絶対温度\(T_i\)は、正確にいうと室内温度\(t_i\)+273℃となります。
実際のところ、室内温度が変化すれば\(T_i\)も変化しますが、ほぼ定数であるとみてよいでしょう。
定数を考えなくて良いとすると、一番初めの圧力差換気との違いは、圧力差\(\Delta P\)が高低差hと温度差\((t_i-t_o)\)に変わっただけです。
温度差及び高低差による換気量の大小関係は、

\(\LARGE 換気量=窓面積\sqrt{高低差×温度差}\)

と表すことができます。

練習問題

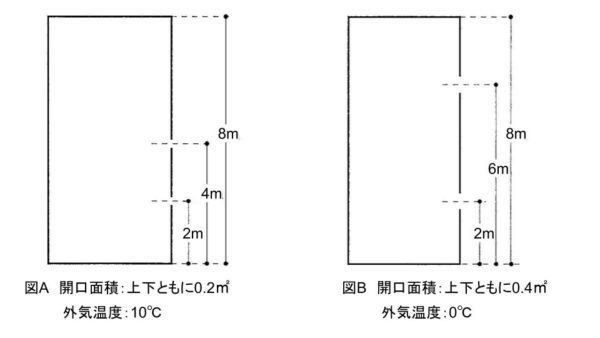
図A、Bは、それぞれ建物の鉛直断面を示したものである。図Aに示す建物の換気量を\(Q_A\)とするとき、 図Bに示す建物の換気量として、最も近いものは、次のうちどれか。ただし、図A、図Bともに室温温は20°Cで、建物外部は無風、開口部の流量係数は全て等しいとする。

1.\(\sqrt{2}Q_A\)
2.\(2Q_A\)
3.\(4Q_A\)
4.\(8Q_A\)

<解答>
一見難しそうですが、今日このブログで勉強したことをフルに生かせば簡単に解けます。
まず、大小関係を聞いているだけなので式を簡略化することが可能です。
そして温度と窓の高低差が聞かれているので使う式は、

\(\large 換気量=窓面積\sqrt{高低差×温度差}\)

になります。

後は図Aの換気量を1と考えた場合、図Bは何倍の換気量があるのかを考えます。
図Aから図Bでそれぞれ何が変化しているかを整理すると、
開口部は2倍（A:0.2㎡　B:0.4㎡）
高低差は2倍（A：2ｍ　B：4ｍ）
温度差は2倍（A：10℃　B：20℃）
変化しています。

これを簡略化した式に代入すると、

\(\large 換気量=2倍\sqrt{2倍×2倍}\)
\(\large 換気量=4倍\)

となります。

答え　3.　\(4Q_A\)　

まとめ