今回は構造の基礎を学習していきたいと思います。
私が受験生だった時、試験まで3ヶ月しかないという無謀なスケジュールだったため、構造の計算問題は捨てる覚悟で受けました。
結果的には公式を暗記して答えられる問題はしっかり得点できたので合格することができました。
一級建築士を取得してからは講師という立場になり、ずっと計画、環境、法規を教えてきましたが、構造に関しては全く触れてこなかったのでほとんど理解がないといっても間違いではありません。
しかしこれからは自らのスキルを向上させるため、構造に関しても教えられる講師を目指して改めて勉強していくことを決めました。
受験生の気持ちになって、わからないところを一つずつ理解していこうと思います。
私が0から勉強するにあたって、日頃からいろいろと手伝って頂いている構造の先生に構造力学のポイントを教えてもらいます。
普段は構造の講師をしています。
また「速学」の構造の解説も担当しています。
私も受験生の時は構造が苦手だったので、苦手な人がどこでつまずいてしまうのか、よくわかります。
難しいところを、なるべくわかりやすく解説できるように頑張りますのでよろしくお願いします。
モーメント
モーメント:物体を回転させようとする力(回転力)をモーメントという。力の大きさPに回転中心から作用線までの垂直距離\(l\)をかけたもの。
\(M=P・l\)

接点の種類
剛節点:部材と部材が強固に接合され、角度が変化しない節点。
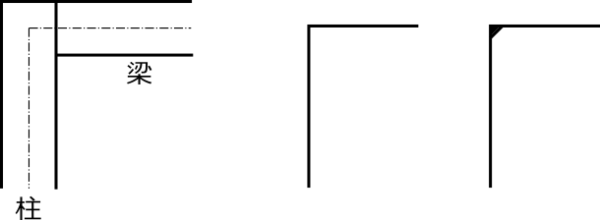
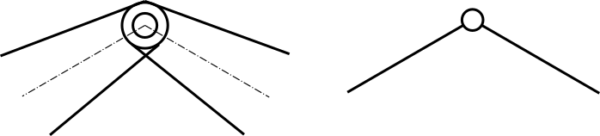
ピン節点:部材と部材が接合されているが、部材同士が角度を変えることができる節点。
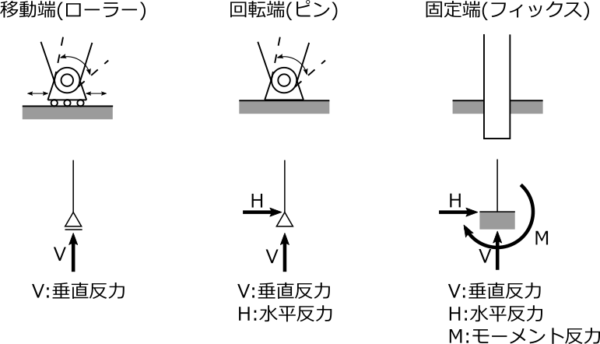
支点と反力
反力:支点の移動や回転を拘束するときに、その支点に生じる力やモーメントをいう。
力のつり合い
力のつり合い:物体に複数の力が同時に作用して、移動も回転もしないで静止しているとき、力はつり合っている。この時、下式が成り立つ。
ΣX=0 X方向の力の総和
ΣY=0 Y方向の力の総和
ΣM=0 モーメントの総和
水平方向:右向きを「+」、左向きを「-」と仮定。
垂直方向:上向きを「+」、下向きを「-」と仮定。
モーメント:時計回りを「+」、反時計回りを「-」と仮定。
計算の結果が「-」になる場合、仮定した向きとは逆向きとなる。
反力の計算
②力のつり合いを考えて反力を求める
<例題1>
単純梁に図のような荷重が作用する場合の支点の反力を求めよ。
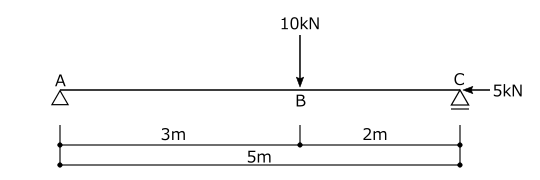
①支点に反力を仮定する
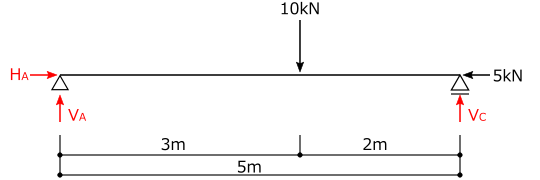
②力のつり合いを考えて反力を求める
ΣX=0より
\(H_A-5=0\)
\(H_A=5\) [kN]
ΣY=0より
\(V_A+V_C-10=0\)
\(V_A+V_C=10\)・・・①
ΣM=0より
\(V_A×5-10×2=0\)
\(V_A=4\) [kN]
①に\(V_A=4\)を代入
\(4+V_C=10\)
\(V_C=6\) [kN]
応力の種類
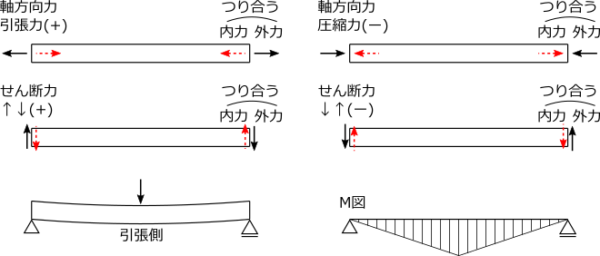
応力:荷重等の外力に対して、部材内で発生する力。応力は部材内のどの位置でも外力とつり合っていると考える。
応力の計算
②力のつり合いを考えて反力を求める
③応力を求めたい点で部材を切断し、片側部分を取り出し、切断面に応力を仮定する。
④力のつり合いを考えて、曲げモーメント、せん断力、軸方向力を求める。
<例題2>
例題1で反力を求めた単純梁のD点の応力を求めよ。
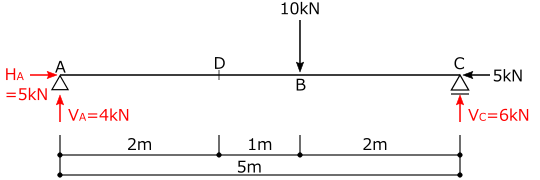
③応力を求めたい点で部材を切断し、片側部分を取り出し、切断面に応力を仮定する。
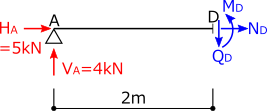
軸力N:引張りになる方向に仮定。
せん断力Q:時計回り(↑↓)になる方向に仮定。
曲げモーメントM:材の下側が引張側になるように仮定。
計算結果が「-」になる場合、仮定した向きとは逆向きになる。
④力のつり合いを考えて、曲げモーメント、せん断力、軸方向力を求める。
ΣX=0より
\(N_D+5=0\)
\(N_D=-5\) [kN]
ΣY=0より
\(-Q_D+4=0\)
\(Q_D=4\)・・・①
Σ\(M_D\)=0より
\(4×2-M_D=0\)
\(M_D=8\) [kN・m]
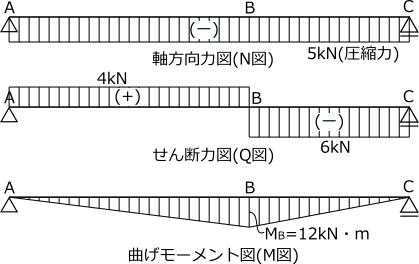
単純梁の応力図
応力図:各点で応力を求め連続的にまとめたもの。
基本をしっかり身につけましょう。
アウトプット型講座 [構造]
構造計算の基本から学べる講座を2/22(土)に開催いたします。
アウトプットを重視した内容になっているので、わからないところを直接、講師の先生に聞くことができます。
講座までにわからないところをまとめて、理解不足の項目を効率よく学習しましょう。
構造力学は手順をしっかり理解すれば、解ける問題が格段に増えます。
この講座で構造計算を得点源にしていきましょう。


